Hidden in Plain Sight: Identifying Cryptography in BLACKMATTER Ransomware
Mandiant
Written by: Jacob Thompson
One of the main goals of evaluating a ransomware sample is to determine what kind of cryptography the sample uses. Sometimes this is straightforward; for a BLACKMATTER sample we analyzed, it was not. We found the process we used to identify the mathematical operations of RSA cryptography from the BLACKMATTER code interesting and reusable for other malware samples and for becoming a better reverse engineer in general.
Introduction
The BLACKMATTER ransomware family has been identified in several recent attacks. Other authors have published summaries of BLACKMATTER, including its relationship to prior families REVIL and DARKSIDE, and method of encryption. Additionally, the U.S. Department of Health and Human Services has published a summary of BLACKMATTER covering historical timeline, associated threat groups, and types of victims.
Mandiant’s FLARE team performed an internal analysis on a 32-bit BLACKMATTER variant (sha256: 5da8d2e1b36be0d661d276ea6523760dbe3fa4f3fdb7e32b144812ce50c483fa). Like many ransomware families, BLACKMATTER uses a combination of symmetric and asymmetric cryptography to hold its victims’ data for ransom. A BLACKMATTER sample has an asymmetric public key inside its configuration, and only the threat actor holds the corresponding private key. When attacking each of a victim’s files, BLACKMATTER first uses symmetric cryptography to encrypt the file. BLACKMATTER then uses the asymmetric public key to encrypt the symmetric key and appends that encrypted key to the end of the file. The symmetric key is then thrown away. The design means that no amount of reverse engineering of the BLACKMATTER binary alone can allow the victim to decrypt the files, because only the attacker’s private key can decrypt the per-file keys and recover the original data.
As we reversed BLACKMATTER, we quickly found its symmetric encryption to be a modified version of Salsa20. The asymmetric cryptography was not as obvious. Ransomware samples often employ a cryptographic library such as Windows wincrypt, OpenSSL, or Crypto++; often the library is statically linked to make it somewhat more difficult to identify. BLACKMATTER was unique and used no identifiable cryptographic libraries. Some cryptographic routines have telltale behaviors—RC4 fills an array of 256 bytes with the values 0 to 255, and Salsa20 performs left rotations of 7, 9, 13, and 18 bits. We did not immediately recognize asymmetric code in BLACKMATTER as a familiar algorithm. Magic numbers can identify cryptographic algorithms, such as ChaCha20’s “expand 32-byte k,” AES’s Te and Td tables, and ASN.1-related byte sequences such as 30 82 02 (or MIIC after base64 encoding); neither did we recognize any magic numbers.
Ultimately, we identified BLACKMATTER’s asymmetric cryptography as 1024-bit RSA, a common and unremarkable choice that we identified partly through the process of elimination (and previous analysis of BLACKMATTER and its predecessor families), but also by locating the mathematical operations employed by BLACKMATTER and connecting them to the raw math behind RSA. It is the process we employed to locate and identify the RSA algorithm that we thought of as interesting and reusable for other malware samples and reverse engineers, and that is the focus of this blog post.
Review of RSA
First, let us begin with a brief review of how RSA works. RSA (Rivest-Shamir-Adleman) is an archetypical cryptosystem for asymmetric cryptography. An individual generates a key pair (public and private key) according to the algorithm; the private key is kept secret while the public key is widely distributed. Among other uses, any party can send the individual a secret message by encrypting the message with the public key and delivering it over an unprotected communication channel. In legitimate use, RSA could be used in e-commerce to establish a shared secret for encrypting information in a credit card transaction. In illicit use like ransomware, RSA is perfectly suited for concealing the information needed to decrypt files until payment is received and then exchanged for the private key.
RSA operates on the principle of modular exponentiation, which is easy to perform but hard to reverse. Here is a greatly simplified explanation of how RSA keys are generated:
- Select two distinct large prime numbers p and q. Let n = pq and ϕ(n) = (p-1)(q-1). n is not secret and may be freely shared as part of the public key, while also knowing ϕ(n) would allow anyone to break the encryption.
- Select an exponent for encryption, e. In practice, e = 65537 is almost always used.
- Determine the corresponding exponent for decryption, d ≡ e-1 (mod ϕ(n)), which is straightforward using the Extended Euclidean Algorithm, but intractable without knowing ϕ(n).
- The pair (n, e) is the public key; d is the private key. Information sufficient to derive d (such as p and q or ϕ(n)) must also be kept secret.
A message may then be encrypted by computing E(m) = me mod n and decrypted by computing D(E(m)) = (me)d mod n ≡ m1(mod n). This property of n, m, e, and d comes from Fermat’s Little Theorem and can be explored by reviewing a more detailed explanation of RSA.
Binary Exponentiation
The choice of e = 65537 is intentional and allows encryption to be performed efficiently while remaining secure. Since e = 65537 = 65536 + 1 = 216+1, m65537mod n can be computed using binary exponentiation as follows:
x=m
for i = 1 to 16:
x = x2mod n
x = xm mod n
Once RSA encryption is distilled to this form, the only complication is that a function is needed to perform “big number” modular multiplication, i.e., f (x, y, n) = xy mod n. Inevitably, while analyzing BLACKMATTER, our attention was diverted to a function which performs modular multiplication, but whose purpose was not obvious. Compounding that, the constant 65537 never appears in the code when implemented as above. Next, we present an explanation showing how we verified how each asymmetric cryptographic function in the BLACKMATTER sample fit in as part of the RSA encryption process.
Multiplication Function
The multiplication of two unsigned binary integers can be expressed as a series of additions and multiplications by two, e.g.:
145 ∙ 113
145 ∙ (26+25+24+20)
(145 ∙ 22 + 145 ∙ 2 + 145) ∙ 24 + 145 ∙ 20
((145 ∙ 2 + 145) ∙ 2 + 145) ∙ 2 ∙ 2 ∙ 2 ∙ 2 + 145
Since a multiplication by two is just a left bit shift by one bit, this makes it possible to multiply x ∙ y using only left shifts and additions, examining each bit of x to determine whether y should be added into the running product on each iteration before shifting the running product to the left. The BLACKMATTER big number multiplication function sub_401B24 (x, y, n), based on this exact principle, calculates x = (x * y) % n.
Of course, x86 machines do not have 1024-bit registers or immediate values, so an operation on a 1024-bit integer must be broken down into 32 operations on each 32-bit chunk of the 1024-bit integer. The x86 instructions rcl, adc, and sbb make such big number arithmetic possible, using the carry flag to propagate a 0- or 1-bit to the next 32-bit chunk as appropriate.
First, the big number multiplication function allocates some stack space for a temporary 1024-bit integer z to hold the running product, and initializes it to zero (Figure 1).
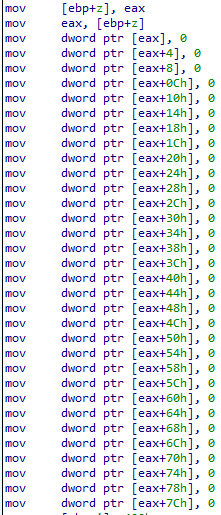

Figure 1: The big number multiplication function starts by initializing a 1024-bit integer z to zero
Next, the big number multiplication function loops over each bit in its inputs and outputs. For each iteration, the function first shifts z left by one bit (Figure 2).
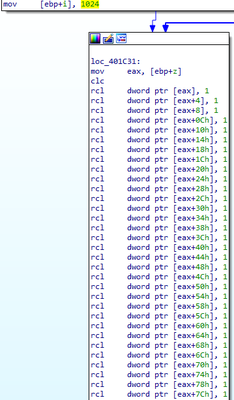

Figure 2: The big number multiplication function shifts z to the left by one bit. Since z is 1024 bits long, the rcl instruction allows the shift to be done on each 32-bit chunk
This calculation multiplies z by two, and therefore may cause z to exceed n. To ensure the calculation is performed mod n, the function next subtracts n from z (Figure 3).
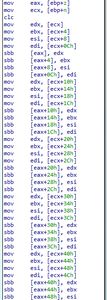

Figure 3: After doubling z, the big number multiplication must subtract n from z to ensure the calculation is done mod n
Note that the malware did not check whether z ≥ n before performing the subtraction, so if the result was negative, the function adds n to z to reverse the previous subtraction and restore z to the range [0, n) (Figure 4). The malware operates this way because comparing z to n before performing the previous subtraction would have been just as computationally expensive as performing the subtraction.


Figure 4: If z -= n produced a negative result, n is added back to z to restore z to the correct range mod n
Now, the function shifts x to the left by one bit. The formerly leftmost bit of x is then left in the carry flag. If the bit was 1, y is added to z; if it was 0, y is not added to z (Figure 5).
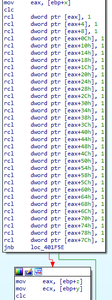

Figure 5: The big number multiplication function shifts x to the left by one bit and uses the formerly-leftmost bit to determine whether y should be added to the running product z on this iteration
In either case, z is again restored into the range [0,n) so that all calculations remain mod n. This process continues for 1024 iterations. Put another way, x is examined bit-by-bit to determine whether or not y should be added to the intermediate product z on each iteration before it is shifted. After all the iterations, x is overwritten with the product z (Figure 6).
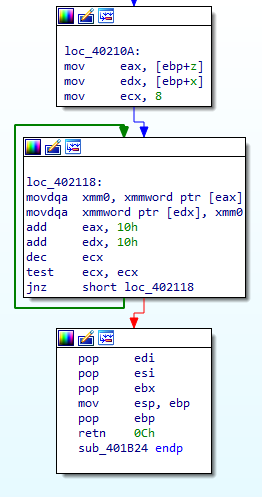

Figure 6: The value x is overwritten with the running product z once the calculation is complete
Note that sub_401B24 can be used to calculate x2mod n by calling sub_401B24(x, x, n).
Binary Exponentiation Function
We found that the big number multiplication function previously described was repeatedly called by what we analyzed to be a binary exponentiation function, sub_4019C0 (x, buf, n, m). This binary exponentiation function computes x = x256mod n if m is NULL, or x = mx256mod n if m is not NULL. When the binary exponentiation function squares x eight times, and optionally multiplies by m, the binary exponentiation function makes nine separate calls to the big number multiplication function in an “unrolled” fashion, making its purpose slightly more difficult to identify. Here is an excerpt of the IDA pseudocode from the binary exponentiation function:
const __m128i *__stdcall sub_4019C0 (const __m128i *x, __m128i *buf, int n, int m)
{
…
x0 = x;
y0 = buf;
i0 = 8;
do
{
*y0++ = _mm_load_si128 (x0++) ;
--i0;
}
while ( i0 );
y1 = buf;
x1 = x;
sub_401B24((__m128i *)x, (int)buf, (_DWORD *) n);
i1 = 8;
do
{
*y1++ = _mm_load_si128(x1++);
--i1;
}
while ( i1 );
...
y8 = buf;
x8 = x;
result = sub_401B24 ((__m128i *)x, (int) buf, (_DWORD *) n);
if ( m )
{
i8 = 8;
do
{
*y8++ = _mm_load_si128 (x8++);
--i8;
}
while ( i8 );
return sub_401B24 ((__m128i *) x, m, (_DWORD *) n);
}
return result;
}
RSA Encryption Function
With the pieces put together, now we can understand the RSA encryption function in BLACKMATTER that wraps the other routines. The RSA encryption function sub_40183C (m, n) encrypts m by calculating m=m65537mod n. As individual steps it operates as follows:
- Let buf and x be 1024-bit integers, and let x = 1.
- Call the binary exponentiation function sub_4019C0 (x, buf, n, m) to calculate x = mx256 mod n, which, since x = 1, is just x = m.
- Call the binary exponentiation function sub_4019C0 (x, buf, n, 0) to calculate x = x256 mod n.
- Call the binary exponentiation function sub_4019C0 (x, buf, n, m) to calculate x = mx256 mod n
At the end of these steps, x = m(m256)256 mod n = m65537mod n.
Here is an excerpt of the IDA pseudocode from the overall RSA encryption function:
__m128i *__stdcall sub_40183C(__m128i *m, __m128i *n)
{
…
x [0] .m128i_i64 [1] = 0i64;
memset (&x [1], 0, 112);
x [0] .m128i_i64 [0] = 1i64;
sub_4019C0 (x, buf, n, m);
sub_4019C0 (x, buf, n, 0);
sub_4019C0 (x, buf, n, m);
px = x;
pm = m;
i = 8;
do
{
*pm++ = *px++;
--i;
}
while ( i );
return px;
}
Since Python natively supports big number integers, the entire BLACKMATTER calculation could be simplified in Python as follows:
x = m
for i in range (16):
x = x * x % n
x = x * m % n
Conclusion
In analyzing BLACKMATTER we found that the author accomplishes RSA encryption with only three freestanding functions with no external libraries. The RSA public key does not stand out as it is simply a 1024-bit integer in the binary. There are no magic numbers—not even 65537—because of how the code is structured; the number 65537 is implicit in performing the sixteen squarings followed by one final multiplication by m; it is possible the author used inline assembly within the three routines. We hope the reader will find these observations useful in spotting RSA implementations in other malware. We also found an insightful reminder in that instead of obscuring the meaning of code through obfuscation and packing, an attacker can also hide it in plain sight by creating freestanding and minimalistic implementations of cryptographic algorithms with no external dependencies.
