Optimize your applications using Google Vertex AI Vizier
Sebastien Soudan
Senior Architect - F5
Laurent Querel
Distinguished Engineer - F5
Businesses around the globe are continuing to benefit from innovations in Artificial Intelligence (AI) and Machine Learning (ML). At F5, we are using AI/MI in meaningful ways to improve data security, fraud detection, bot attack prevention and more. While the benefits of AI/ML for these business processes are well articulated, at F5, we also use AI/ML to optimize our software applications.
Using AI/ML for better software engineering is still in its early days. We are seeing use cases around AI assisted code completion, auto-code generation for no-code/low-code platforms but we are not seeing broad usage of AI/ML in optimizing the software application architecture itself. In this blog, we will demonstrate workload optimization of a data pipeline using black-box optimization with Google’s Vertex AI Vizier.
Performance Optimization
Today, software optimization is an iterative and mostly manual process where profilers are used to identify the performance bottlenecks in software code. Profilers measure the software performance and generate reports that developers can review and further optimize the code. The drawback of this manual approach is that the optimization depends on developer's experience and hence is very subjective. It is slow, non-exhaustive, error prone and susceptible to human bias. The distributed nature of cloud native applications further complicates the manual optimization process.
An under-utilized and more global approach is another type of performance engineering that relies on performance experiments and black-box optimization algorithms. More specifically, we aim to optimize the operational cost of a complex system with many parameters. Other experiment-based performance optimization techniques exist, such as causal profiling, but are outside the scope of this post.
As illustrated in Figure 1, the process to optimize the performance is iterative and automated. A succession of controlled trials is performed on a system to study the value of a cost function characterizing the system to be optimized. New candidate parameters are generated, and more trials are performed until this results in too little improvement to be worthwhile. More details on this process later in this post.
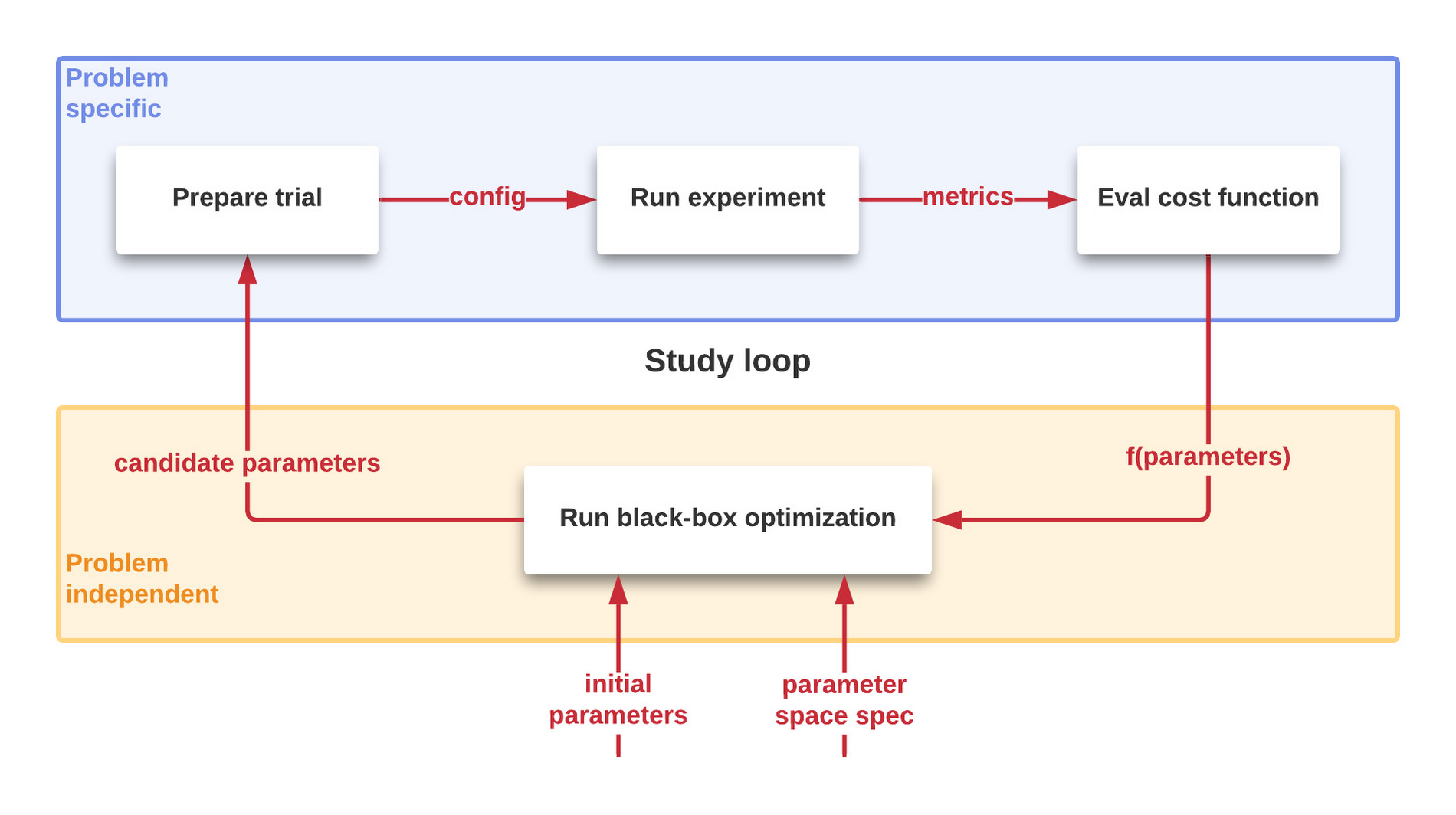

What is the problem
Let's first set the stage - partly inspired by our experience, partly fictitious for the purpose of this discussion.
Our objective is to build an efficient way to get data from PubSub to BigQuery. Google Cloud offers a fully managed data processing service, Dataflow for executing a wide variety of data processing patterns which we use for multiple other realtime streaming needs. We opted to leverage a simplified custom stream processor for this use case for processing and transformations to benefit from the 'columnar' orientation of BQ — sort of 'E(t)LT' model.
The setup for our study is illustrated in more detail in Figure 2. The notebook in the central position plays the role of orchestrator for the study of the 'system under optimization'. The main objectives (and components involved) are:
Reproducibility: in addition to an automated process, a pub/sub snapshot is used to initialize a subscription specifically created to feed the stream processor to reproduce the same conditions for each experiment.
Scalability: the Vertex AI Workbench implements a set of automated procedures used to run multiple experiments in parallel with different input parameters to speed up the overall optimization process.
Debuggability: for every experiment the study and trial ids are systematically injected as labels for each log and metric produced by the stream processor. In this way, we can easily isolate, analyze, and understand the reasons for a failed experiment or one with surprising results.
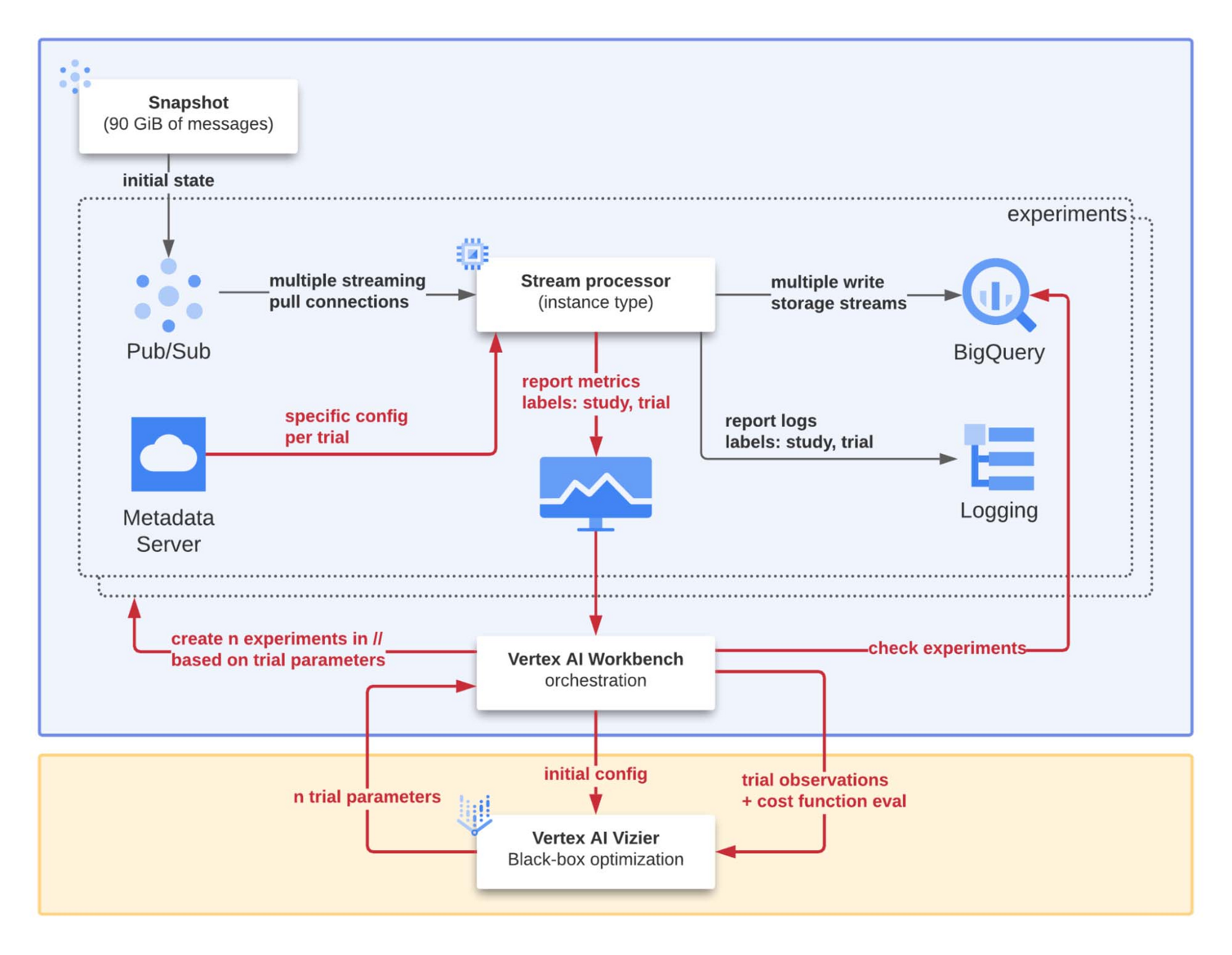

To move the data from PubSub to BigQuery efficiently, we designed and developed some code and now want to refine it to be as efficient as possible. We have a program, and we want to optimize based on performance metrics that are easy to capture from running it. Our question now is how do we select the best variant?
Not too surprisingly, this is an optimization problem: the world is full of them! Essentially, these problems are all about optimizing (minimizing or maximizing) an objective function under some constraints and finding the minima or maxima where this happens. Because of their widespread applicability, this is a domain that has been studied extensively.
The form is typically:
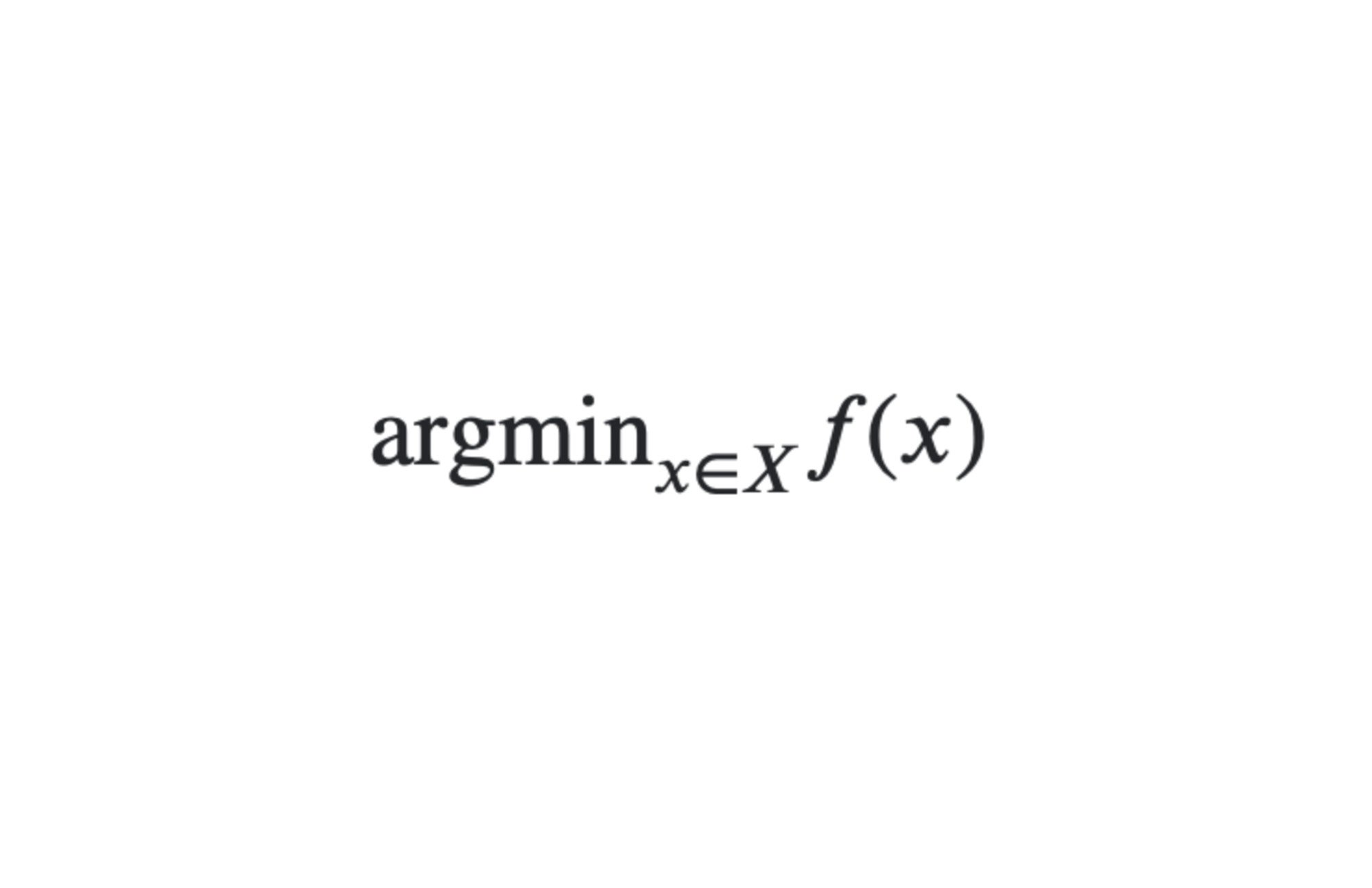
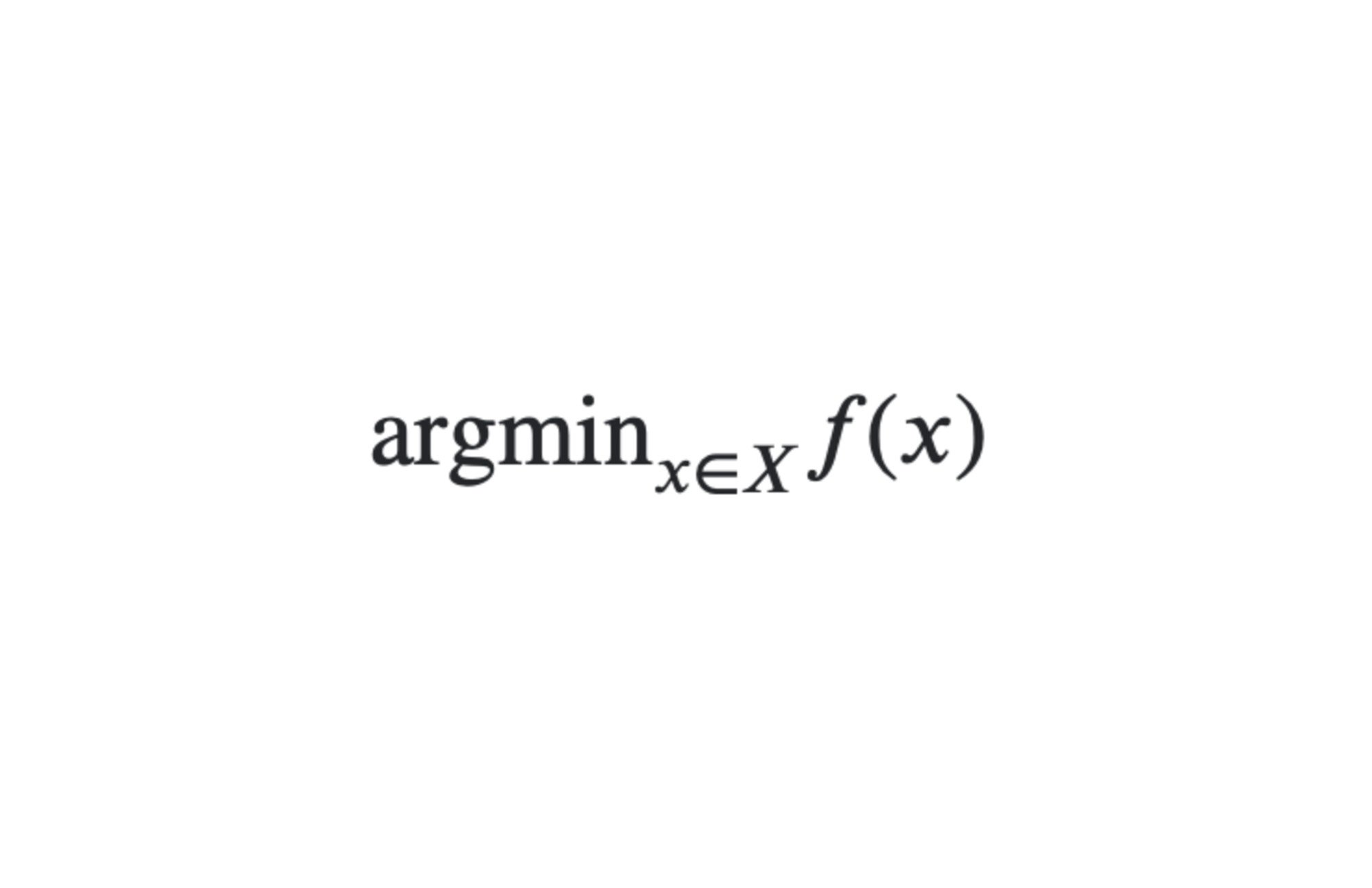
- read as we want the x of a certain domain X that minimizes a cost function f. Since it is a minimization problem here, such x are called minima. Minima don’t necessarily exist and when they do are not necessarily unique. Not all optimization problems are equal: continuous and linear programming is 'easy', convex optimization is still relatively easy, combinatorial optimization is harder... and this is assuming we can describe the objective function we want to optimize — even partially as with being able to compute gradients.
In our case, the objective function is some performance (still TBD at this point) of some program in some execution environment. This is far from f(x)=x2: we have no analytical expression for our program performance, no derivatives, no guarantee that the function is convex, the evaluation is costly, and the observation can be noisy. This type of optimization is called 'black-box optimization' for the reason that we cannot describe it in simple mathematical terms our objective function. Nonetheless we are very much interested in finding the parameters that deliver the best result.
Let's now frame our situation as a concrete optimization problem before we introduce further black-box optimization and some tools as we are looking for a way to automate solving this type of problems rather than doing it manually — 'time is money' as they say.
Framing as an optimization problem
Our problem has many moving parts but not all have the same nature.
Objective
First comes the objective. In our case, we want to minimize the cost per byte of moving data from PubSub to BigQuery. Assuming that the system scales linearly in the domain we are interested in, the cost per byte processed is independent of the number of instances and allows to extrapolate precisely the cost to reach a defined throughput.
How do we get there?
We run our program on a significant and known volume of data in a specified execution environment — think specific machine type, location, and program configuration —, measure how long it takes to process it and calculate the cost of the resources — named `cost_dollar` below. This is our cost function f.
As mentioned earlier, there is no simple mathematical expression to define the cost function of our system and evaluating it actually involves running a program and is 'costly' to evaluate.
Parameter space
Our system has numerous knobs: the program has many configuration parameters corresponding to alternative ways of doing things we want to explore and sizing parameters such as different queue size or number of workers. The execution environment defines even more parameters: VM configuration, machine type, OS image, location, ... In general, the number of parameters can vary wildly — for this scenario, we have a dozen.
In the end, our parameter space is described by Table 1 which for each `parameter_id` gives the type of value (integer, discrete or categorical).
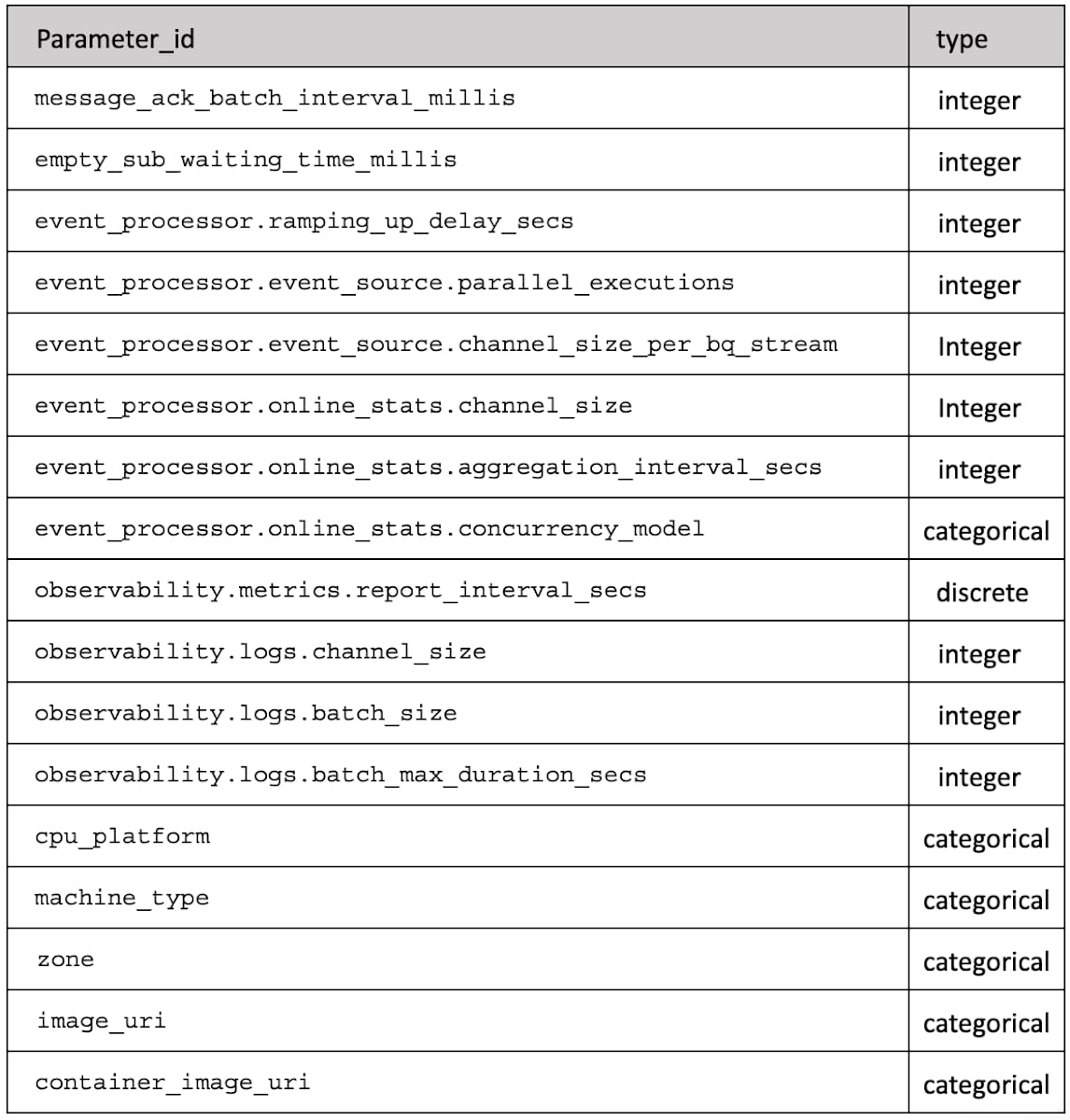

The objective has been identified, we know how to evaluate it for some given assignment of a collection of identified parameters and we have defined the domain of these parameters. That's what we need to allow us to do some black-box optimization.
Approach
Back to the black-box optimization: we already stated this is a problem dealing with minimization/maximization of a function for which we have no expression, we can still evaluate it! We just need to run an experiment and determine the cost.
The issue is running the experiment has a cost and given the parameter space, exploring them all is rapidly not a viable option. Assuming you pick only 3 values for each of the 12-ish parameters: 312=531,441 — it's large already. This method of exploring systematically all the combinations generated from a subset of each parameter taken individually is called grid search.
Instead, we use a form of surrogate optimization: In case like this one where there is no convenient representation of our objective function, it can be beneficial to introduce a surrogate function with better properties that models the actual function. Certainly, instead of one problem: minimizing our cost function, we have two: fitting a function on our problem and minimizing it. But we gained a recipe to move forward: fit a model on the observations and use this model to help choose a promising candidate for which we need to run an experiment. Once we have the result of the experiment, the model can be refined and new candidates can be generated, until marginal improvements are not worth the effort.
Google Cloud Vertex AI Vizier offers this type of optimization as a service. If you want to read more about what is behind — spoiler: it relies on Gaussian Process (GP) optimization, check this publication for a complete description: Google Vizier: A Service for Black-Box optimization.
We performed 148 different experiments with different combinations of input parameters. What have we learned?
Results of our study
The point of this discussion is not to detail precisely what parameters we used to get the best cost - this is not transferable knowledge as your program, setup, and pretty much everything will be different. But to give an idea of the potential of the method: in our case, with 148 runs, our cost function went from $0.0780/run with our initial guessed configuration down to $0.0443/run with the best parameters — a reduction of the cost of 43%. Unsurprisingly, the `machine_type` parameter plays a major role here, but even with the same machine type as the one offering the best results, the (explored) portion of our cost function ranges between $0.0443/run and $0.0531/run - a variation of 16%.
The most promising runs are represented in Figure 3. All axes but the last 2 correspond to parameters. The last two, respectively, the objective `cost_dollar`, and represent whether the run completed or not. Lines represent the runs and connect the values for each axis together corresponding to them.
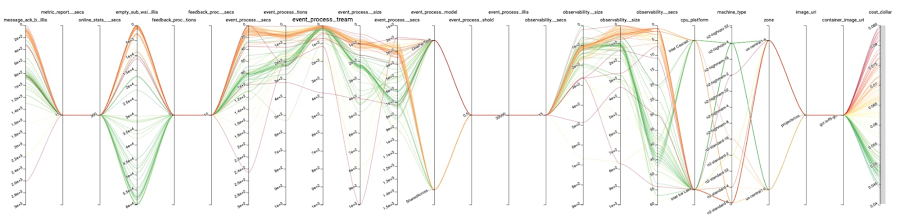

To conclude on the study part, this helped us uncover substantial cost improvement with almost no intervention from our end. Let's explore that aspect more in the next section.
Learnings on the method
One of the main advantages of this method is that: provided you have been through the initial effort of setting things up suitably, it can run on its own and require little to no human intervention.
Black-box optimization assumes the evaluation of f(x) only depends on x not on what else is going on at the same time.
We don't want to see interactions between the different evaluations of f(x).
One of the main applications of Vizier is deep learning model hyper-parameter optimization. The training and evaluation are essentially devoid of side effects — cost aside, but we already said black-box optimization methods assume the evaluation is costly and are designed to reduce the number of runs needed to find the optimal parameters. Our scenario has definitively side-effects: it is moving data from one place to another.
So, if we ensure all side-effects are removed from our performance experiment, life should be easy on us. Black-box optimization methods apply, and Vizier in particular can be used. This can be achieved by wrapping the execution of our scenario in some logic to setup and tear down an isolated environment: making this whole new system essentially without side-effect.
Couple of lessons on running these kinds of tests we think worth highlighting:
Parameterize everything even if there is a single value at first: if another value becomes necessary it is easy to add, worst case: values are recorded along with your data making it easier to compare things between different experiments if needed.
Isolation between runs and other things: if it is not parameterized and have an impact on the objective, this will make the measurements noisier and make it harder for the optimization process to be decisive about where to explore next.
Isolation between concurrent runs: so can run multiple experiments at once.
Robust runs: not all combinations of parameters are feasible, and Vizier supports reporting them as so.
Enough runs: Vizier leverages the result of previous runs to decide what to explore next and you can request for a number of experiments to run at once - without having to provide the measurement yet. This is useful to start running experiments in parallel but in our experience this is also useful to make sure initially you have a broad coverage or the parameter space before the exploration starts to try to pinpoint local extrema. For example, in the set of runs we described earlier in the post, 'n2-highcpu-4' didn't get tried until run 107.
Tools exist today: Vizier is one example available as a service. There are many python libraries available too to do black-box optimization.
Definitely something to have in your toolbox if you don't want to spend hours with knobs and you prefer a machine doing that.
Conclusion and next steps
Black-box optimization is unavoidable for ML hyper-parameter tuning. Google Vertex AI Vizier is a black-box optimization service with a wider range of applications. We believe it is also a great tool for the engineering of complex systems that are characterized by many parameters with essentially unknown or difficult to describe interactions. For small systems, manual and/or systematic exploration of the parameters might be possible, but the point of this post is that it can be automated!
Optimizing performance is a recurring challenge as everything keeps changing and new options and/or new usage patterns appear.
The setup presented in this post is relatively simple and very static. There are natural extensions of this setup to continuous online optimization that are worth exploring from a software engineering perspective like multi-armed bandits.
What if the future of application optimization was already here but not very evenly distributed - to paraphrase William Gibson?
Think this is cool? F5 AI & Data group hires!



